Ⅵ-1 Nice Chain の基本(New)
<スポンサード リンク>
〔1〕 Nice Chain の位置付け
前章の有段の手筋・達人の手筋では、2択連鎖を活用した各種手筋を紹介してきましたが、下表のように、これらをさらに集約・統合した上位手筋が、名人の手筋 Nice chain となります。
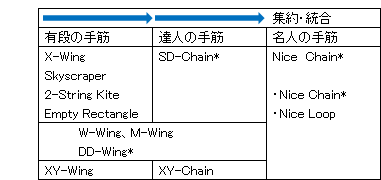
Nice Chain と、Nice Chain に包含される全ての手筋は、『2択連鎖』という共通の考え方で統一され、2択連鎖の仕組みを理解する事が、幅広い解法手筋の修得につながります。
Nice Chain の手筋名称については、本サイトでは2択連鎖を活用した Chain系 を中心に紹介している事により、一般的な名称との対応は以下のようになります。
| 区分 | 本サイト | 一般的名称 | |
| 総称 | Nice Chain | Nice Loop | |
| Chain系 |
Nice Chain (≒AIC) |
Discontinuous Nice Loop 又は AIC(Alternate Inference Chain) |
|
| Loop系 | Nice Loop | Continuous Nice Loop |
ここで2択連鎖とは、2択となる数字のペアが次々と鎖のように繋がったもので、2択の数字ペアは大別すると、①如意棒、②2値マス、③ER・PLブロックの3種類があります。

①如意棒
縦列・横行またはブロック内で、ある数字の入る可能性が2マスに限定される場合の2択。
如意棒の両端の数字が2拓の選択肢となり、以降の説明では左図のように表現します。

②2値マス
1つのマスに入る可能性の有る数字が、2つの数字に限定される場合の2択。
マス内の2つの数字が2拓の選択肢となり、以降の説明では左図のように表現します。

③ER・PLブロック
ブロック内で、グループ化された数字の2択
上段:ERブロック
下段:PLブロック
青・赤線で囲った2組の3連数字が2択の選択肢で、表現上は、左図のように如意棒と同様になります。
〔2〕 2択の特性と、連鎖への活用
2択とは、「2つある選択肢の中から、どちらか1つを選ぶこと」、2者択一の省略形という事ですが、ここでは、さらに、下記のような特性を持つものとして考えていきます。

2択連鎖の仕組みでは、Bの特性が有効に働き、2択同志を次々と連結していく事ができます。
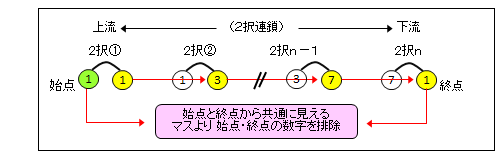
下図例では、先頭の2択①の下流側が「真」としてスタート。以降、2択の上流側が打ち消されて「偽」となり、下流側が全て「真」となることで連鎖が継続していきます。

つまり、始点(緑)と、下流側の各々の黄色は、全て2択の関係になるというのが、攻略手筋の基本的な考え方として重要なポイントになります。
次に、上図の2択連鎖の具体的な例を示します。(如意棒3本と、2値マス2個の5連鎖)

11<B7・B2> + 33<B2・E2> = 33<E5・H5> = 35<H8> = 51<D8>
B列の2択の如意棒に着目し、下流側のB2=1の場合、上右図のように2択の上流側が打ち消されて、下流側が全て真となります。(B2=1の場合は、同時にD8=1となるのがポイント)
この為、始点B7=1または、終点D8=1のどちらかが真の2択となり、共通に見える灰色5マスから数字1が排除されます。(Skyscraper の排除マスと同様の原理)
〔3〕2択の連結パターン
2択連鎖が継続していく2択の連結パターンとしては、隣接する数値が同じ<同値連結>と、数値が異なる<異値連結>が有ります。

◆同値連結
隣接する2択同志を、共通の数値を介して連結する方法で、如意棒・2値マス・ERブロック等をブロック間、又はブロック内で連結する事で、2択連鎖の一部を構成することができます。
隣接する2択の数値同志を連結する場合は、ブロック間、又は、ブロック内で、お互いが直接見えるマス位置に配置される事が必要です。

11<C8・C1> = 13<B2> = 33<右上> = 33<H5・E5> = 35<E9> = 51<F7>
上図は如意棒・2値マス・ERブロックの2択6連鎖の例で、各2択の間は同じ数値で連結されています。そして、C列2択の下流側C1=1の場合は、以降連鎖を辿って、F7=1となります。
この為、始点C8=1または、終点F7=1のどちらかが真の2択となり、共通に見える灰色5マスから数字1が排除されます。(Skyscraper の排除マスと同様)
◆異値連結
2本の如意棒の片端同士を、1つのマス内で共有して連結する方法で、2択連鎖の一部を構成することができます。但し、数値の異なる如意棒同志のマス内連結に限定されます。

11<B2・B5> + 33<B5・B8> + 55<B8・E8> + 77<E8・E4> + 11<E4・H4>
上図は如意棒をマス内で連結した2択5連鎖の例で、各2択の間は異なる数値で連結されています。そして、始点の下流側B5=1の場合は、以降連鎖を辿って、H5=1となります。
この為、始点B2=1または、終点H5=1のどちらかが真の2択となり、共通に見える灰色マスから数字1が排除されます。(2-String Kite の排除マスと同様)
この異値連結では、2択の如意棒の一方が、同じマス内の別の数値で打ち消される事で、連鎖が継続していく点に特徴があります。
◆同値・異値の混合連結の例
同値・異値連結は、2択連鎖の中で混在して使用でき、如意棒・2値マス・PLブロック等の組み合わせも、連結位置が正しければ自由に行えます。

11<B8・B5> + 33<B5・B2> = 33<中上> = 37<H3> = 77<H5・D5> = 77<F6・F8>
上図は如意棒・PLブロック・2値マスの2択6連鎖の例で、各2択間は同値・異値が混合連結されています。そして、始点の下流側B5=1の場合は、連鎖を辿ってF8=7となります。
この為、始点B2=1または、終点F8=7のどちらかが真となり、始点と終点のマスがお互いに見える位置にある為、B8から7、F8からは1が排除されます。(DD-Wing の解法より)
〔4〕2択連鎖の解法手筋への応用
2択連鎖を活用した Nice Chain の解法手筋は、Chain系・Loop系の2系統に大別され、本サイトでは、それぞれ Nice Chain、及び、Nice Loop として説明していきます。
◆Nice Chain
Chain系では、2択連鎖の始点・終点のどちらかが必ず真となる、という特性を利用して、共通に見えるマスからある数字を排除する、というのが基本的な攻略手法になります。
そして、2択連鎖の始点・終点の数字を各々X・Zとすると、X=Z、X≠Z のどちらかと、始点・終点のマス配置により、3種類の解法パターンに分れます。
Nice Chain は、一般的に AIC(Alternate Inference Chain)と呼ばれる手筋となります。
◆Nice Loop
2択連鎖の両端が繋がり、どの2択が起点でも、右回り・左回りどちらからも矛盾なく連鎖が継続するとき、連鎖全体がLoop 状になり、Nice Loop が成立します。

2択同志の連結部(同値・異値連結)から多くの排除マスが検出されるため、攻略が一気に進む可能性があります。そして、この手筋は一般的に continuous Nice Loop と呼ばれます。
〔5〕2択連鎖の表記方法
2択連鎖とは、2択となる数字のペアが次々と鎖のように繋がったもの、と説明してきましたが、この連鎖を説明するのに便利な表記方法について、本サイトでの記法を以下に示します。

2択①、2択② 等の 2択n は、基本的に "2択の数値<マス位置>" と記述,。
連結子は、同値連結が "="、異値連結が "+" と記述しますが、具体例を下記に示します。

如意棒は、まず両端の数字2個を書き、続いて<>の中に両端のマス位置を書きます。B列の例 : 33<B5・B2>
2値マスでも、まず2値マスの2つの数値を書き、次に<>内にマス位置を1つ書きます。H3の2値マス例 : 37<H3>
中上・右下のPL・ERブロックでは、まずグループ化された2択の数値を2個書き、続いて<>内にブロックの位置を、
"左中右" 、続けて、 "上中下 "のように2文字で表現します。
上図は、如意棒2本とPLブロック・2値マス・ERブロックの2択5連鎖の例で、この連鎖全体の表記を下記に示します。

"|"の後ろは排除マスの記述ですが、必要に応じて追加します。"<>"は≠と同じ意味。
左中右を"LMR "(Left、Middle、Right)、上中下を "TMB"(Top、Middle、Bottom)でもOK。

◆ループ型での2択連鎖の表記例
@ 11<B8・B5> + 33<B5・B2> = 37<H2> = 71<H8> = @
先頭と最後が"@"で繋がり、最後の連結子が "=" の場合は同値連結、"+" の場合は異値連結となります。
左図は、2択4連鎖のループ型で、 Nice Loop の解法により、灰色マスからマス内に書かれた数字が排除され、水色マスからは1・3以外の数字が排除されます。
 南碁空の
ナンプレ攻略の広場
南碁空の
ナンプレ攻略の広場